
Formative assessment, developmental stages and starting the year well
The goal of formative assessment should always be to find out what each student NEEDS next, rather than focusing
Misconceptions in maths behave an awful lot like conspiracy theories
Conspiracy theories exist to some extent in all societies and are seemingly at odds with what we think we know from cognitive load theory about how people learn. Surely if an explanation was clear enough, step-by-step and built carefully in complexity, then we would be able to avoid conspiracy theories in the first place? Or at least combat them before they became embedded or widespread? Yet this is clearly not the case.

Conspiracy theories are often sparked by an observation, noticing or wondering. An idea develops, leading to an assumption that seemingly explains the observation. We’ve found a pattern! Now, we seek to confirm it… rather than looking for evidence that we might be wrong… or even checking to make sure that the original observation or assumption is correct. Confirmation bias is strong. It leads us to over-generalise ideas and creates a firm conviction that is not likely to change without a very good reason and a significant amount of discomfort.
Lecturing won’t do that – we will either argue back, or simply nod and smile until the lecturer leaves… so how does relate to maths?
Misconceptions and alternative conceptions have a lot in common with conspiracy theories. They start with a student’s own observation – an intuitive assumption that they have made by themselves, rather than something they were taught (Swan, 2001). That means that the student thinks their idea is logical (Sneider and Ohadi, 1998), and it also means that we can’t avoid them by careful explanation or instruction (Hansen, 2014). That makes misconceptions really hard to overcome (Ryan & Williams, 2007). They are resistant to explicit instruction, persisting even when the students are actively engaged and got the right answers at the point of instruction (Taylor and Kowalski, 2014; Lyddy and Hughes, 2012).
Misconceptions persist because they come from the child’s own observation and experience.
By way of example, imagine a situation in which the initial fractions that a student has experienced are halves, then quarters, then eighths. From this, they might observe that fractions are formed by halving, so assume that this is always the case (Kennedy, 2016). So, perhaps decimal numbers are formed by halves or quarters? Or to make thirds we might fold the paper into half and half again, then select three of the subsequent bits? This assumption would make it difficult to remember that 0.7 is 7 tenths rather than 7 quarters, and that “seven tenths” is the same as 0.7 and 7/10.

So, if misconceptions come from the child’s own observation or assumption, then students need an opportunity to grapple with a discrepancy or anomaly to provoke them into questioning their own thinking.
It’s not likely to be pretty – in fact, discomfort is a necessary part of the process.
We need to create a low-stakes environment in which they can experiment safely with their own ideas, making and testing conjectures, without pressure to be “efficient” or even “accurate” first time around. Otherwise, those over-generalisations will just be papered over until they sit a test that doesn’t closely match our instruction, like NAPLAN or PAT Maths, or external exams… or even problem-solving questions that require transfer.
Rather than launching into a new topic with a “frantic catch up lesson”, in which we try to rapidly reteach all the previously taught-but-forgotten content, consider swapping that one lesson for a problem-solving question. It doesn’t take any more time, but does make the learning stick. The problem needs to be tricky enough that students don’t immediately know how to solve it, so that it acts as formative assessment.
A good task is one that is closed, but makes kids think hard because it is a little unusual or just new (Kennedy, 2023). The wording should not be tricky and the numbers should be kept low to balance cognitive load. Ideally, we want a question that encourages students to guess at the answer, then have to experiment to actually work it out. An example is shown below, along with three examples of common initial responses from year 7 and 8 students.
Start by encouraging students to make a conjecture (have a guess), and award each with a point.
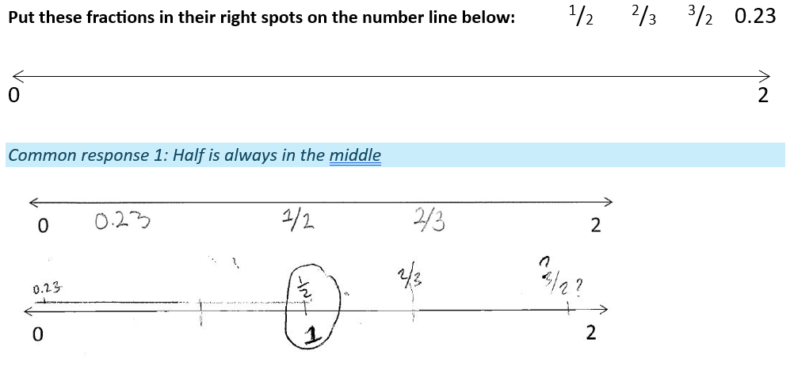

The next step is to encourage students to test their conjectures out, highlighting any discrepancies as we go along to provoke a little discomfort. As this can be really frustrating, the testing itself should earn another point.
This is the “evaluating” process within reasoning.
One way to do this is to ask questions that put a student into cognitive conflict. These questions focus on comparisons (bigger, smaller, same), rather than asking a student to justify why they came up with that answer.
As the lesson is introduced as an opportunity to experiment, students can be encouraged to “prove or disprove” all conjectures.
One way to do this is to write all the initial guesses on the board, then form pairs or threes and work through them, starting with the conjecture made by children in the group. It works really well as an initial lesson even if the students do not end up solving the problem, because the cognitive conflict created tends to mean that they are far more ready to hear our explanations in the next lesson.
Delaying the explanation until the following lesson seems to work better than showing the solution immediately, as it bugs them over night. The experiment also provides students with an opportunity to practise mathematical thinking and activates retrieval of prior learning… plus we have the added bonus of finding out just what we are dealing with so that we can target our instruction in the lessons that follow.
Recent research has shown that spending time teaching to student errors is more effective than explicit instruction for improving results in high-stakes exams in senior school (Metcalfe et. al, 2024).
Another recent example showed that a balanced teaching that began with an experimental problem improved the progress rate on PAT M by 75% over three years (Kennedy, 2023).
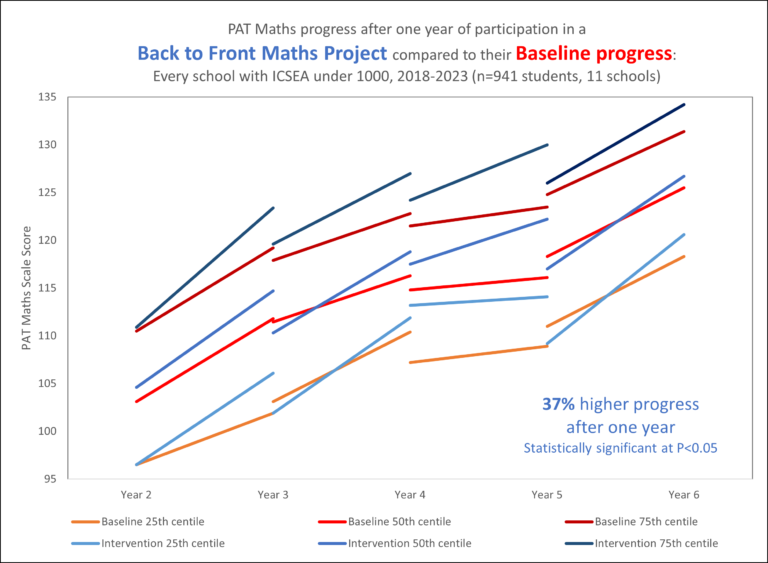
As a third example, the graph below shows the change in PAT M progress for 11 schools working on this approach, all with ICSEA values below 1000. The graph compares the baseline progress (red) from the year before beginning this approach with the same schools’ progress one year later (n=941 students, 11 primary schools). They made 37% faster progress compared to their previous levels.
Misconceptions matter.
Just like conspiracy theories, they persist after explanations, because they come from the student. Introducing experimental problems prior to instruction give us a super power – both to know why students are stuck and to help challenge the underlying ideas that block retention.
Why not try it out with your kids?
Download our Fractions test here to try with your kids.
Hansen, A. (2014). Children’s errors in mathematics (3rd Edition). Los Angeles: SAGE
Kennedy, T. (2016). Interventions in mathematics: Fixing misconceptions in fractions. Townsville: Kennedy Press
Kennedy, T. (2023). Improving learning rates on standardised testing through a balanced teaching cycle: a tale of three schools. Teaching Mathematics, April 2023, pp.10-17. QAMT Available here: https://www.backtofrontmaths.com.au/wp-content/uploads/2023/06/QAMT-article-a-tale-of-three-schools.docx
Lyddy, F., & Hughes, S. (2012). Attitudes towards psychology as a science and the persistence of psychological misconceptions in psychology undergraduates. In V. Karandashev & S. McCarthy (Eds.), Teaching around the world (Vol. 3). Newcastle upon Tyne, UK: Cambridge Scholars Publishing.
Metcalfe, J., Xu, J., Vuorre, M., Siegler, R., Wiliam, D., & Bjork, R. A. (2024). Learning from errors versus explicit instruction in preparation for a test that counts. British Journal of Educational Psychology, 00, 1–15. https://doi.org/10.1111/bjep.12651
Ryan, J. and Williams, J. (2007). Children’s mathematics 4-15: Learning from errors and misconceptions. Berkshire: Open University Press
Swan, M. (2001). Dealing with misconceptions in mathematics. In: P. Gates (Ed.) Issues in Mathematics Teaching (pp.147-165). London: RoutledgeFalmer
Sneider, C. I. & Ohadi, M. M. (1998). Unraveling students’ misconceptions about the Earth’s shape and gravity. Science Education. 82, 265 – 284.
Taylor, A. and Kowalski, P. (2014). Student misconceptions: Where do they come from and what can we do? In V. Benassi, C. Overson and C. Hakala (Ed.s) Applying Science of Learning in Education: Infusing Psychological Science into the Curriculum. New Hampshire: American Psychological Association.

The goal of formative assessment should always be to find out what each student NEEDS next, rather than focusing
Recently I’ve been pondering findings from a major report into Australian schooling that kids who are struggling in maths by

Enabling prompts or life lines are a fantastic way of helping students who are stuck to get started. They do not reduce

Pie charts are an awesome way of linking statistics, fractions and angles, however they can often be difficult for students

While it may sound counter-intuitive, the easiest way to learn to tell the time is to remove the minute hand
Hundreds charts are great for connecting tens and ones. Why not turn one into a jigsaw puzzle to use in

KENNEDY PRESS PTY LTD
FOR ALL ENQUIRIES, ORDERS AND TO ARRANGE PD:
© COPYRIGHT 2023 KENNEDY PRESS PTY LTD ALL RIGHTS RESERVED TERMS & CONDITIONS