
Formative assessment, developmental stages and starting the year well
The goal of formative assessment should always be to find out what each student NEEDS next, rather than focusing
Multiplicative thinking is one of the concepts that I have found about 1 in 4 primary teachers across the country are missing… and I have tried the diagnostic tasks below with several thousand of them. Along with Place Value and Proportional Reasoning, Multiplicative thinking is one of the most important concepts to square away in primary school, yet surprisingly few adults have it.
Why don’t you try out this two-step task with your staff (or for yourself) to see what happens? The results might shock you.
I have found that huge numbers of teachers end up with 615 for this question instead of 805. There are often a few other answers as well, but I consistently find that at least 25% of primary teachers get 615. This is achieved by multiplying 20 x 30 (600) and 3 x 5 (15) then adding these together.
But now here’s the killer…
I have found that over 90% of teachers who get 615 draw a picture with “groups of” or additive model (e.g. 3 circles with 5 dots in each, tally marks – see the picture at the bottom of this post). On the other hand, teachers who end up with 805 almost exclusively draw an array or grid (3 rows of 5, or 5 rows of 3).
If you have ended up with 615, try drawing 23 x 35 as an array (rectangle or grid-structure instead of groups-of structure) and seeing what it looks like. Once you have your rectangle, divide the side with 23 into a 20 and a 3 part. Draw a line or fold your rectangle to show the two different parts. Then repeat with the 35 side, breaking the 35 into a 30 part and a 5 part. You will find that you have now broken your rectangle into four parts that are different sizes and shapes. The smallest part is 3 x 5. The largest part is 20 x 30. Those are the two that you used in working out 615 as an answer. Which parts are you missing?
What is happening?
Picturing multiplication as arrays or grids is a pivotal point in the development of student thinking. If our conceptual understanding of multiplication is additive or linear in nature (such as counting in numbers or picturing a groups of model) then we find it very difficult to develop the underlying patterns and principles of mathematics past that point. We need to be able to picture multiplication of numbers in two-dimensions in order to:
Typical teaching methods for multiplication:
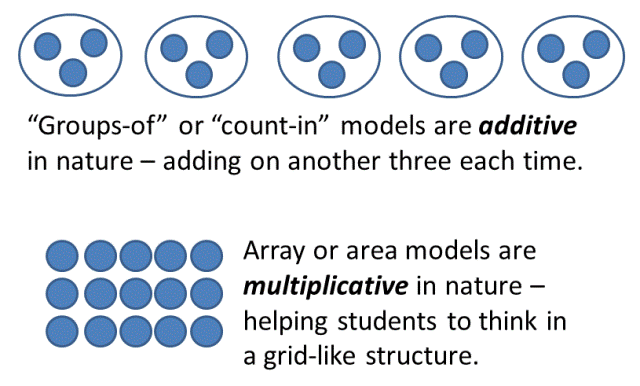
We often use Skip Counting and a Group-of model to introduce multiplication, yet these are both additive or linear models. They don’t really work for numbers bigger than 10 and they can’t be used to see the commutative properties of multiplication. A much more powerful model is to use arrays from the very start. By arranging our groups into a grid we can simultaneously see both terms and the product. We can still count in each term (e.g. 3, 6, 9, 12, 15 or 5, 10, 15) but we can also see the link between the two.
Why not using arrays next time you are introducing multiplication?

The goal of formative assessment should always be to find out what each student NEEDS next, rather than focusing
Recently I’ve been pondering findings from a major report into Australian schooling that kids who are struggling in maths by
Developing algorithms is an important area in AC9, and one that is new to many teachers.But what does it mean
Organising your classroom can be tricky, especially when behaviour is an issue. Here are two layouts that I find work,

Extension can be a tricky issue to deal with. While we can try to have extension questions for most in-class
Setting the scene for risk-taking One of the most difficult problems to overcome when establishing a problem-based classroom is encouraging

KENNEDY PRESS PTY LTD
FOR ALL ENQUIRIES, ORDERS AND TO ARRANGE PD:
© COPYRIGHT 2024 KENNEDY PRESS PTY LTD ALL RIGHTS RESERVED TERMS & CONDITIONS